


Next: Specifying the System
Up: Quantum Computation and Nonlinearity
Previous: Quantum Computation and Nonlinearity
In [4] we found a mathematical formulation of a quantum
neural network through a quantum dot molecule coupled to the substrate
lattice through optical phonons, and subject to a time-varying external
field. In this case, the nonlinearity is a consequence of the real-time propagation of the
system coupled to its environment. Dissipation is not considered
here, although the general model can incorporate this possibility [6,4].
Using discretized Feynman path integrals, authors found that the real time
evolution of the system can be put into a form which resembles the equations
for the virtual neuron activation levels of an artificial neural
network. The timeline discretization points serve as virtual neurons.
Through the Feynman path integral formulation of quantum mechanics we can
write the expression for the time evolution of the quantum mechanical state
of a system as:
![\begin{displaymath}
\exp \left( \frac{i}{%%TCIMACRO{\UNICODE[m]{0x127}}
\rlap{...
...) \right] \right) \mid \psi \left( x_{0},0\right) \rangle .
\end{displaymath}](img52.png) |
(5) |
Expression (5) is equivalent to the following one:
![\begin{displaymath}
\exp \left( \sum\limits_{j=0}^{N}\left[ \frac{im\Delta t}{2...
...ht)
\right] \right) \mid \psi \left( x_{0},0\right) \rangle
\end{displaymath}](img54.png) |
(6) |
Here
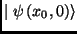 is the input state of the
quantum system at time
is the input state of the
quantum system at time 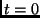 and
and
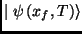 is the output state at time
is the output state at time 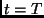 . In this equation,
. In this equation, 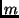 is the mass,
is the mass,
![$2\pi
\rlap{\protect\rule[1.1ex]{.325em}{.1ex}}h$](img60.png) is Planck's constant, and
is Planck's constant, and 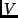 is the potential energy. In the second line,
the paths are discretized:
is the potential energy. In the second line,
the paths are discretized: 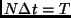 , with the number of discretization
points,
, with the number of discretization
points,
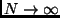 .
.



Next: Specifying the System
Up: Quantum Computation and Nonlinearity
Previous: Quantum Computation and Nonlinearity
Gilson Giraldi
2002-07-02
![\begin{displaymath}
\mid \psi \left( x_{f},T\right) \rangle =\int\limits_{\left...
...eft( x_{f},T\right) }D\left[ x\left( t\right) \right] \times
\end{displaymath}](img51.png)
![\begin{displaymath}
\mid \psi \left( x_{f},T\right) \rangle =\int\limits_{\left...
...eft( x_{f},T\right) }D\left[ x\left( t\right) \right] \times
\end{displaymath}](img51.png)
![\begin{displaymath}
\begin{array}[t]{c}
lim \\
N \rightarrow \infty
\end{ar...
...325em}{.1ex}}h\Delta t}\right) ^{\left( N-1\right) /2}\times
\end{displaymath}](img53.png)