

Next:A
Quantum Dot NeuralUp:Models
for Quantum NeuralPrevious:Classical
Neural Networks
Quantum Computation and Nonlinearity
In practice, the most useful model for quantum computation is the Quantum
Computational Network also called Deutsch's model [5,9].
The basic information unit in this model is a qubit, which can be
considered a superposition of two independent states 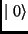 and
and 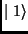 , denoted by
, denoted by 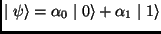 ,
where
,
where 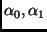 are complex numbers such that
are complex numbers such that 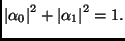 A composed system with
A composed system with  qubits is described using
qubits is described using 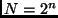 independent states obtained through the tensor product of the Hilbert Space
associated with each qubit. Thus, the resulting space has a natural basis
that can be denoted by:
independent states obtained through the tensor product of the Hilbert Space
associated with each qubit. Thus, the resulting space has a natural basis
that can be denoted by: 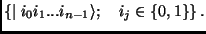 This set can be indexed by
This set can be indexed by 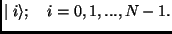 Following the Quantum Mechanics Postulates, the state of the system
Following the Quantum Mechanics Postulates, the state of the system 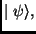 in any time
in any time 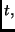 can be expanded as:
can be expanded as: 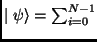
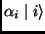 and
and 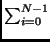
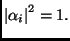 The computation unit in Deutsch's model consists of quantum gates which
are unitary operators that evolves an initial state performing the necessary
computation to get the desired result (final state). A quantum computing
algorithm can be summarized in three steps: (1) Prepare the initial state;
(2) A sequence of quantum gates to evolve the system; (3) Quantum measurements.
From quantum mechanics theory, the last stage performs a collapse and only
what we know in advance is the probability distribution associated to the
measurement operation. So, it is possible that the result obtained by measuring
the system should be post-processed to achieve the target (the Deutschïs
Algorithm (Chapter 6 of [9])
is a nice example). Let us return to the perceptron model of section 2.
Would it be possible to implement a system analogous with it but based
on quantum mechanics? Just as a matter of setting ideas, let's take the
quantum inspired perceptron model proposed in [1].
In this model a quantum system with
The computation unit in Deutsch's model consists of quantum gates which
are unitary operators that evolves an initial state performing the necessary
computation to get the desired result (final state). A quantum computing
algorithm can be summarized in three steps: (1) Prepare the initial state;
(2) A sequence of quantum gates to evolve the system; (3) Quantum measurements.
From quantum mechanics theory, the last stage performs a collapse and only
what we know in advance is the probability distribution associated to the
measurement operation. So, it is possible that the result obtained by measuring
the system should be post-processed to achieve the target (the Deutschïs
Algorithm (Chapter 6 of [9])
is a nice example). Let us return to the perceptron model of section 2.
Would it be possible to implement a system analogous with it but based
on quantum mechanics? Just as a matter of setting ideas, let's take the
quantum inspired perceptron model proposed in [1].
In this model a quantum system with 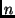 input qubits
input qubits 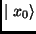 ,
, 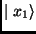 ,...,
,..., 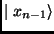 is considered and an output is derived by the rule:
is considered and an output is derived by the rule:
 |
(3) |
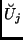 are
are 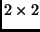 matrices acting on the basis
matrices acting on the basis 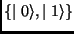 .
In analogy with the classical perceptron, the following learning rule is
proposed:
.
In analogy with the classical perceptron, the following learning rule is
proposed:
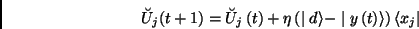 |
(4) |
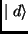 is the desired output. It can be shown [1]
that the above rule drives the system into desired state
is the desired output. It can be shown [1]
that the above rule drives the system into desired state 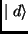 .
From the quantum mechanics point of view, the first problem of the above
system is that the learning rule in expression (4)
is not an unitary operation in general (the same is true for expression
(3)).
That is way we call this model quantum inspired. Besides, ANNs need
activation functions, which are scalar and nonlinear functions, to be implemented.
Nonlinear effects in quantum computation are discussed by Gupta at al.
[5]
when they proposed a new gate - a dissipative one- called D-Gate.
The behavior of the D-Gate is the following: given the state system
.
From the quantum mechanics point of view, the first problem of the above
system is that the learning rule in expression (4)
is not an unitary operation in general (the same is true for expression
(3)).
That is way we call this model quantum inspired. Besides, ANNs need
activation functions, which are scalar and nonlinear functions, to be implemented.
Nonlinear effects in quantum computation are discussed by Gupta at al.
[5]
when they proposed a new gate - a dissipative one- called D-Gate.
The behavior of the D-Gate is the following: given the state system 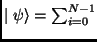
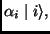 let
let 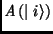 and
and 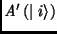 respectively denote the probability amplitudes before and after the application
of the D operator. Then, if
respectively denote the probability amplitudes before and after the application
of the D operator. Then, if 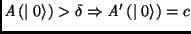 ;
otherwise
;
otherwise 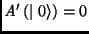 .
The value
.
The value 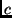 for probability amplitude denotes some constant used for encoding
for probability amplitude denotes some constant used for encoding 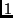 and
and 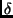 is a pre-set threshold. From the point of view of Gupta at al. [5]
we could postulate a quantum neural network constructed from Unitary operators
and the D-Gate. In the network representation, the quantum gates are interconnected
by wires indicating the information flow during the computation (see Figure
2).
By convention, the computation proceeds from left to right.
is a pre-set threshold. From the point of view of Gupta at al. [5]
we could postulate a quantum neural network constructed from Unitary operators
and the D-Gate. In the network representation, the quantum gates are interconnected
by wires indicating the information flow during the computation (see Figure
2).
By convention, the computation proceeds from left to right.
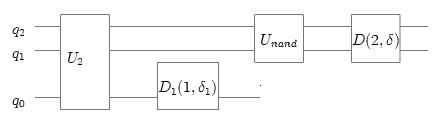
|
Figure 2: Outputs are connected to Gates
inputs in the network.
However, a quantum mechanics feasible learning rule should be designed
to complete the QNN. This point is not addressed by Gupta at al.
To answer this question we need a more deeply consideration about the
D-Gate and its hardware implementation. This is the starting point of our
work. The D-Gate nonlinearity is due to dissipations. Such irreversible
operation can be realized if full interaction with the environment is taken
into account. The behavior of a system can also be nonlinear because of
the interactions between its degrees of freedom (see sections 5, 6 of [5]).
But, what kind of physical system in quantum mechanics can perform nonlinear
operations?
What about learning rules? The expression (4)
gives a rule that adapts operators which evolves the state of the system.
However, in the classical perceptron, the quantities affected by the learning
rule (2)
are system parameters! Quantum mechanical systems have in general a set
of pre-defined parameters. Could be a learning rule that adapts system
parameters more feasible in practice? Is there such a rule? We believe
that a possible (may be partial) solution for these questions is the model
stated next.
Subsections


Next:A
Quantum Dot NeuralUp:Models
for Quantum NeuralPrevious:Classical
Neural Networks
Gilson Giraldi 2002-07-02

