


Next: Training the Quantum Network
Up: Quantum Computation and Nonlinearity
Previous: A Quantum Dot Neural
The formulation above is general. A QNN approach comes out when the system is
that of a quantum dot molecule with five dots arranged as the pips on a
playing card. The dots are close enough to each other that
tunneling is possible between any two neighbors. Two electrons are fed into
the molecule, which then has a doubly-degenerate ground state (in the
absence of environmental potentials). These states can be thought of as the
polarization 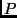 of the molecule, equal to
of the molecule, equal to 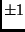 , that is, the Pauli
matrix operator
, that is, the Pauli
matrix operator 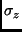 . In Equation (5) this would be the value
. In Equation (5) this would be the value
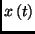 .
In addition to adjusting or training
.
In addition to adjusting or training
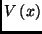 , we
can obtain an
additional trainable nonlinearity by coupling the system to its
environment. The environment is modeled by a set of Gaussians, that is, the
environment has a quadratic Hamiltonian, or, equivalently, a normal
distribution; if the set is taken to be infinite, any desired influence
including dissipation can be produced. In this model this would be
represented by the coupling between the electronic state of the dot
molecules and the lattice through optical phonons. Physically the coupling
would have to be weak enough to be represented accurately as linear; for
example, GaAs substrate satisfies this, with a (unitless) electron-phonon
coupling parameter of
, we
can obtain an
additional trainable nonlinearity by coupling the system to its
environment. The environment is modeled by a set of Gaussians, that is, the
environment has a quadratic Hamiltonian, or, equivalently, a normal
distribution; if the set is taken to be infinite, any desired influence
including dissipation can be produced. In this model this would be
represented by the coupling between the electronic state of the dot
molecules and the lattice through optical phonons. Physically the coupling
would have to be weak enough to be represented accurately as linear; for
example, GaAs substrate satisfies this, with a (unitless) electron-phonon
coupling parameter of 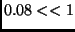 .
Instead of taking
.
Instead of taking
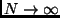 like in (6), we take
like in (6), we take 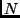 to be finite (quasi-continuum). Equation (6) becomes:
to be finite (quasi-continuum). Equation (6) becomes:
![\begin{displaymath}
I\left[ \sigma _{z}\left( \Delta t\right) \right] \mid \psi \left( \sigma
_{z}\left( 0\right) ,0\right) \rangle
\end{displaymath}](img73.png) |
(7) |
where the path integral over possible positions at each time, 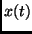 , has
been written as a finite set of sums over states of the polarization,
, has
been written as a finite set of sums over states of the polarization,
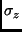 , at each time slice
, at each time slice 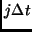 . Also, at each time slice the
polarization can be either
. Also, at each time slice the
polarization can be either 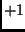 or
or 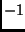 . The potential energy
. The potential energy 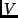 comes from
a time-varying electric field,
comes from
a time-varying electric field,
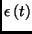 , and the kinetic
energy term, in this two-state basis, now has the form
, and the kinetic
energy term, in this two-state basis, now has the form
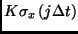 , where
, where 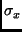 is the Pauli matrix. Since
is the Pauli matrix. Since 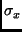 is off-diagonal in the polarization basis, this term contains the
(nonlinear) coupling between the states of the quantum dot molecule at
successive time slices. The size of this term, given by the parameter
is off-diagonal in the polarization basis, this term contains the
(nonlinear) coupling between the states of the quantum dot molecule at
successive time slices. The size of this term, given by the parameter 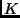 (the tunneling amplitude), is determined by the physics of the dot molecule:
how easy it is for the electrons to tunnel from polarization state
(the tunneling amplitude), is determined by the physics of the dot molecule:
how easy it is for the electrons to tunnel from polarization state 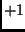 to
to 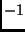 . The effect of the optical phonons is summarized by the influence
functional
. The effect of the optical phonons is summarized by the influence
functional
![$I\left[ \sigma _{z}\left( t\right) \right] $](img83.png) , given by:
, given by:
![\begin{displaymath}
I\left[ \sigma _{z}\left( t\right) \right] =\int \prod_{k}D...
....1ex}}h}\int\limits_{0}^{T}d\tau \sum\limits_{k}S_{k}\right)
\end{displaymath}](img84.png) |
(8) |
where
and 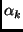 is the position variable of the
is the position variable of the 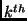 harmonic
oscillator (phonon),
harmonic
oscillator (phonon), 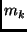 its mass,
its mass, 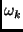 its frequency, and
its frequency, and
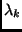 its coupling strength to the system. The advantage of a
linearly coupled harmonic bath is that the path integrals over the phonons
can be performed immediately, giving us the nonlinear functional:
its coupling strength to the system. The advantage of a
linearly coupled harmonic bath is that the path integrals over the phonons
can be performed immediately, giving us the nonlinear functional:
![\begin{displaymath}
I\left[ \sigma _{z}\left( t\right) \right] =\exp \left(
\s...
...right) \sigma _{z}\left( j^{\prime
}\Delta t\right) \right)
\end{displaymath}](img91.png) |
(9) |
where
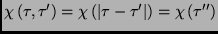 is the influence phase, proportional to the response function of the bath.
For the phonon bath,
is the influence phase, proportional to the response function of the bath.
For the phonon bath,
![\begin{displaymath}
\left[ \cosh \left( \frac{\beta %%TCIMACRO{\UNICODE[m]{0x12...
..._{k}}{2}\right) \sin \left( \omega _{k}\tau \right) \right]
\end{displaymath}](img94.png) |
(10) |
where it was introduced also a (suitably low) temperature, given by 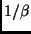 in units of Boltzmanns constant.
In [4] authors consider the obtained
in units of Boltzmanns constant.
In [4] authors consider the obtained 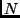 intermediate states
to be the states of
intermediate states
to be the states of 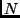 virtual quantum neurons, one at each time
slice
virtual quantum neurons, one at each time
slice 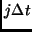 . The nonlinearity necessary for neural computation is
inherent in the kinetic energy term,
. The nonlinearity necessary for neural computation is
inherent in the kinetic energy term,
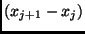 , and in
the exponential. Each of the
, and in
the exponential. Each of the 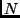 neurons different possible states
contributes to the final measured state; the amount it contributes, can be
adjusted by changing
the potential energy,
neurons different possible states
contributes to the final measured state; the amount it contributes, can be
adjusted by changing
the potential energy,
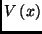 .
The trainable parameters set can be any of those that appear above (
.
The trainable parameters set can be any of those that appear above (
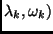 or even the values of the electric field at each time
slice
or even the values of the electric field at each time
slice 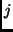
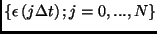 .
Combinations of these sets are also possible to be trained. It is important
to emphasize that any of these parameters can be physically controlled
[4].
.
Combinations of these sets are also possible to be trained. It is important
to emphasize that any of these parameters can be physically controlled
[4].
Subsections



Next: Training the Quantum Network
Up: Quantum Computation and Nonlinearity
Previous: A Quantum Dot Neural
Gilson Giraldi
2002-07-02
![\begin{displaymath}
\sum_{\left\{ \sigma _{z}\left( j\Delta t\right) \right\} }...
...t) \sigma _{z}\left( j\Delta t\right) \right] \right) \times
\end{displaymath}](img72.png)
![\begin{displaymath}
\chi \left( \tau \right) =\sum\limits_{k}\frac{\lambda _{k}...
...ect\rule[1.1ex]{.325em}{.1ex}}h\omega _{k}}{2}\right) \times
\end{displaymath}](img93.png)