CanonDefine.html

CanonDefine.mws

Function: Canon[CanonDefine] - Define symmetries of a tensor (or an indexed object)

Calling Sequence:
CanonDefine(tensor, rank, symmetries, base);

Parameters:
tensor - the tensor name (without indices)

rank - the number of indices

symmetries - a set of permutations (signed or not) representing the tensor symmetries or the names Symmetric or AntiSymmetric

base - (optional) base for the the generating set.

Description:

CanonDefine is used to define the symmetries of a given tensor. CanonDefine assigns the symmetries and base to the respective entry in the internal CanonSymmetryTable.

The first argument is the name of the tensor. The second is the number of indices. The third argument is a set of permutations or minus signed permutations that generate the symmetries of the tensor. The fourth argument is optional. It is the base for the symmetry generating set. The standard base is [1,2,...], where the element is the number of indices.

There are 2 special symmetries that CanonDefine accept as third argument: Symmetric or AntiSymmetric, which represent totally symmetric or antisymmetric tensors respectively. In this case the number of arguments must be 3 (the base is the standard one).

If the set of permutations is not a strong one, it is automatically completed by applying a procedure for obtaining a strong generating set. A base is also generated if CanonDefine is issued with 3 arguments.

A minus-signed permutation is represented by a list, where the first element is -1, and the second element is a list of lists describing the permutation, e.g. [-1, [[1,3],[2,4]]].

If the output is 0 then the symmetries generate a vanishing tensor.

> with(Canon):

The following defines a tensor of rank 3 symmetric in the last 2 indices:

> CanonDefine(T, 3, {[[2,3]]});

The following defines the symmetries of the Riemann tensor:

> CanonDefine(R, 4, {[-1,[[1,2]]],[-1,[[3,4]]],[[1,3],[2,4]]});

The following defines a totally symmetric tensor of rank 5:

> CanonDefine(S, 5, Symmetric);

Checking the symmetries:

> print(CanonSymmetryTable);

Next command is equivalent to state: T[b,a]=-T[b,a], which implies a vanishing tensor.

> CanonDefine(Z, 2, {[[1,2]],[-1,[[1,2]]]});

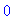
See Also: CanonPrint , CanonUnPrint , Canonical , CanonicalOne