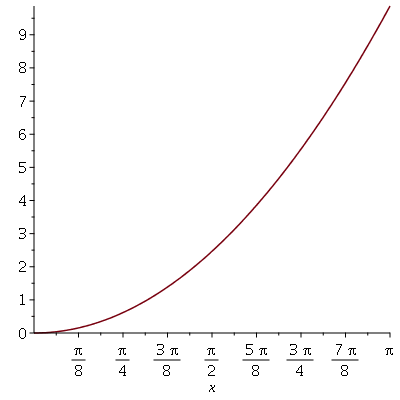
Definindo uma Função e Calculando a Derivada
O Maple tem uma grande variedade de funções definidas internamente, incluindo as funções trigonométricas, hiperbólicas, elíticas, hipergeométricas, de Bessel e muitas outras. A lista completa pode ser obtida através do help on line com o comando ?
inifcn
. Todos os comandos do Maple, como o comando de integração, de diferenciação, de limite, etc., estão aptos a reconhecer estas funções e fornecer o resultado esperado.
Por maior que seja a lista das funções definidas internamente pelo Maple, um usuário necessita definir suas próprias funções, por exemplo, generalizando funções já existentes. Estas funções definidas pelo usuário serão incluidas na lista das funções do Maple no sentido de que elas também serão reconhecidas pelos comandos de diferenciação, integração, etc., como funções válidas, mas não serão reinicializadas automaticamente caso o usuário sai do Maple ou dê o comando restart. O usuário deve salvar a worksheet e processar os comandos para ativar a função.
Para definir uma função no Maple usamos o operador seta (->), isto é, sinal de menos seguido do sinal de maior. Por exemplo, a função 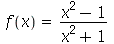 é definida da seguinte maneira.
é definida da seguinte maneira.
| > |
 |
| > |
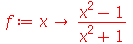 |
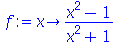 |
(1.1.1) |
Podemos avaliar essa função em um ponto ou encontrar sua derivada com o comando
diff
.
| > |
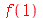 |
 |
(1.1.2) |
| > |
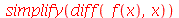 |
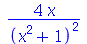 |
(1.1.3) |
Também é possível definir uma função da forma
| > |
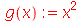 |
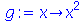 |
(1.1.4) |
desde que escolha function definition na janela que se abre após dar o comando acima. Porém, este método deve ser evitado. Por que? Porque é a maneira errada de definir funções no Maple. Evite!
É importante distinguir uma função (tem variáveis) de uma expressão algébrica (não têm variáveis). Por exemplo, vamos definir expressão algébrica:
| > |
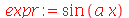 |
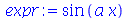 |
(1.1.5) |
No comando acima, 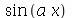 é uma expressão que foi atribuida a variável expr. Não podemos considerar expr como uma função de x, pois não obteríamos o resultado desejado com o comando expr(
é uma expressão que foi atribuida a variável expr. Não podemos considerar expr como uma função de x, pois não obteríamos o resultado desejado com o comando expr( ):
):
| > |
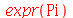 |
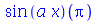 |
(1.1.6) |
O resultado desejado era 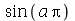 . Para obter o valor da função
. Para obter o valor da função 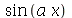 em
em 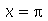 , temos que usar o comando subs ou
algsubs
:
, temos que usar o comando subs ou
algsubs
:
| > |
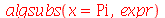 |
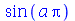 |
(1.1.7) |
Para definir uma verdadeira função a partir uma expressão algébrica já nomeada, devemos usar o comando
unapply
(em vez do operador seta):
| > |
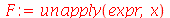 |
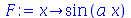 |
(1.1.8) |
Neste caso especificamos que a expressão 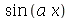 é uma função de
é uma função de 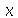 e
e 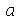 é um parâmetro. Até agora, o Maple não tinha condições de saber se queríamos uma função na variável
é um parâmetro. Até agora, o Maple não tinha condições de saber se queríamos uma função na variável 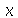 tendo
tendo 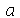 como parâmetro ou vice-versa. Vejamos o que ocorre com esta nova definição:
como parâmetro ou vice-versa. Vejamos o que ocorre com esta nova definição:
| > |
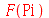 |
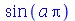 |
(1.1.9) |
| > |
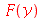 |
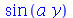 |
(1.1.10) |
| > |
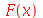 |
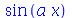 |
(1.1.11) |
ATENÇÃO: Não deixe espaço entre a função e o parêntese esquerdo. Por exemplo, "F (a)" produz um resultado diferente de F(a). "F (a)" quer dizer o produto de F por a.
Assim podemos obter o valor da função em um ponto da forma F(ponto). Podemos dizer que 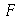 é o nome da função
é o nome da função 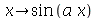 . Vejamos:
. Vejamos:
| > |
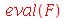 |
 |
(1.1.12) |
Exitem alguns comandos no Maple que têm funções como argumento. Eles não aceitam uma expressão algébrica como argumento. Este é o caso do operador D, que só atua em funções dando como resultado outras funções (a derivada). Por exemplo:
| > |
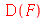 |
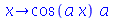 |
(1.1.13) |
O comando acima está com a sintaxe correta. O comando abaixo está com a sintaxe errada.
| > |
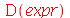 |
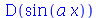 |
(1.1.14) |
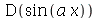 tem a sintaxe errada, pois o operador D está sendo aplicado a uma expressão. Vamos comparar com o operador diff. Este atua em expressões algébricas e também retorna uma expressão algébrica. Por exemplo:
tem a sintaxe errada, pois o operador D está sendo aplicado a uma expressão. Vamos comparar com o operador diff. Este atua em expressões algébricas e também retorna uma expressão algébrica. Por exemplo:
| > |
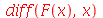 |
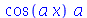 |
(1.1.15) |
Outro comando perfeitamente válido:
| > |
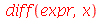 |
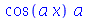 |
(1.1.16) |
A derivada segunda é obtida da seguinte forma
| > |
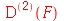 |
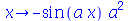 |
(1.1.17) |
Note que os parênteses são obrigatórios. Se os parênteses não forem colocados, obteremos
| > |
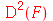 |
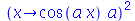 |
(1.1.18) |
que é equivalente a 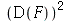 , isto é, o quadrado de
, isto é, o quadrado de 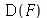 .
.
Vimos que a letra D é usada como operador diferencial. Todos os comandos do Maple estão protegidos contra atribuição. Por exemplo, o comando
| > |
 |
| Error, attempting to assign to `D` which is protected. Try declaring `local D`; see ?protect for details. |
|
retorna um erro. Se o usuário faz questão absoluta de usar D como variável em alguma aplicação, o usuário pode usar o comando
unprotect
para liberar a proteção sobre D. O comando
restart
fará o operador D voltar a ser o que era. O usuário também pode proteger nomes através do comando
protect
.
Como vimos acima, uma outra maneira de definir uma função é usar diretamente o operador seta (-> sinal de menos seguido do maior). Por exemplo:
| > |
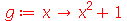 |
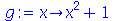 |
(1.1.19) |
| > |
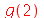 |
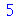 |
(1.1.20) |
Esta forma não é necessariamente equivalente ao comando unapply.
ATENÇÃO: Quando usar o operador seta (->), a expressão da função deve ser dada explicitamente.
Não devemos usar % dentro do operador seta. Veja a seguinte sequência de comandos problemática.
| > |
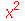 |
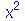 |
(1.1.21) |
| > |
 |
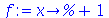 |
(1.1.22) |
| > |
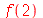 |
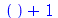 |
(1.1.23) |
O problema ocorreu porque o operador seta não avalia a expressão colocada no lado direito. O objetivo era definir a função 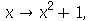 porém o resultado foi catastrófico. Neste caso precisamos usar o comando
unapply
:
porém o resultado foi catastrófico. Neste caso precisamos usar o comando
unapply
:
| > |
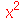 |
| > |
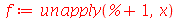 |
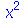 |
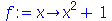 |
(1.1.24) |
| > |
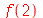 |
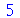 |
(1.1.25) |
Exceção a esta regra é o uso de label da expressão. Por exemplo
| > |
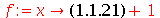 |
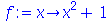 |
(1.1.26) |
| > |
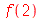 |
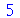 |
(1.1.27) |
Para colocar um label em uma expressão, o usuário deve clicar no INSERIR ou INSERT, clicar em LABEL (gerando um nova janela), e digitar no número do label (com os pontos) no espaço apropriado na janela. Se houver alguma mudança no número de expressões anteriores à linha do label, o número do label é atualizado automaticamente.
É preciso entender que existem alguns comandos no Maple que não avaliam os operandos antes da execução. A maioria dos comandos avaliam os operandos, porém isto também pode ser um problema. Vamos ver um exemplo. Vamos contruir a função que soma o MDC com o MMC de dois números. Por exemplo, o MDC de 25 e 15 é 5 e o MMC é 75, de forma que a função deve retornar 80. Confirmando no Maple:
| > |
 |
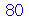 |
(1.1.28) |
Vamos construir duas versões, a primeira usando o comando unapply e a segunda usando o operador seta:
| > |
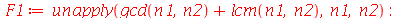 |
| > |
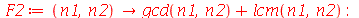 |
| > |
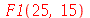 |
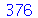 |
(1.1.29) |
| > |
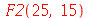 |
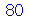 |
(1.1.30) |
Obtivemos o resultado errado com F1. A função foi definida de maneira incorreta e o motivo foi que o comando unapply avaliou os seus argumentos antes de criar a função. A avaliação de 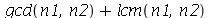 é
é 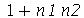 , como podemos verificar:
, como podemos verificar:
| > |
 |
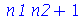 |
(1.1.31) |
De fato:
| > |
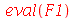 |
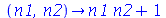 |
(1.1.32) |
A maneira correta de definir esta função usando o comando unapply é:
| > |
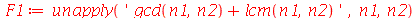 |
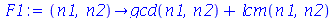 |
(1.1.33) |
| > |
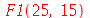 |
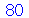 |
(1.1.34) |
A versão com o operador seta não sofre deste problema, pois seus argumentos não são avaliados.
| > |
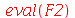 |
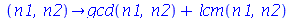 |
(1.1.35) |
Derivada Parcial
A derivada parcial também é calculada com o comando
diff
. Por exemplo, vamos definir uma função de duas variáveis e calcular a derivada parcial em relação ao segundo argumento.
| > |
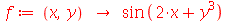 |
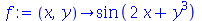 |
(1.2.1) |
| > |
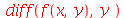 |
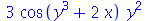 |
(1.2.2) |
Através do operador
D
podemos calcular a "função derivada parcial".
| > |
](images/curso6_100.gif) |
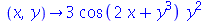 |
(1.2.3) |
Note que quando aplicamos o operador
D
à uma função de duas ou mais variáveis temos que especificar a posição da variável. A derivada parcial de segunda ordem 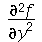 em relação a segunda variável é
em relação a segunda variável é
| > |
](images/curso6_103.gif) |
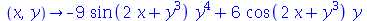 |
(1.2.4) |
A derivada mista 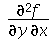 é
é
| > |
](images/curso6_106.gif) |
Para obter a expressão 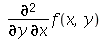 devemos usar a forma
devemos usar a forma
| > |
)(x, y)](images/curso6_108.gif) |
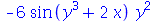 |
(1.2.5) |
Usando o operador D, é possível calcular diretamente a derivada em um ponto, por exemplo
| > |
)(0, 0)](images/curso6_110.gif) |
 |
(1.2.6) |
Isto não é possível de ser feito como o comando diff.
Funções Anônimas
Diversos comandos do Maple usam funções como argumento e muitas vezes é mais econômico usar uma função anônima. Vejamos alguns exemplos. Suponha que temos uma lista com 20 números aleatórios menores ou iguais a 10:
| > |
![L := [seq((rand(1 .. 10))(i), i = 1 .. 20)]](images/curso6_112.gif) |
![[7, 10, 6, 2, 4, 6, 5, 1, 8, 5, 10, 2, 2, 4, 8, 3, 9, 10, 2, 8]](images/curso6_113.gif) |
(1.3.1) |
Queremos selecionar os números são menores que 5.
| > |
 |
![[2, 4, 1, 2, 2, 4, 3, 2]](images/curso6_115.gif) |
(1.3.2) |
Usamos a função booleana anônima 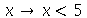 como primeiro operando do comando
select
. O segundo operando deve ser uma estrutura de dados, cujos elementos queremos selecionar. A saída é uma estrutura de dados do mesmo tipo com os elementos que satisfazem à função booleana. Lembre, o primeiro argumento deve ser uma função booleana (retorna false ou true).
como primeiro operando do comando
select
. O segundo operando deve ser uma estrutura de dados, cujos elementos queremos selecionar. A saída é uma estrutura de dados do mesmo tipo com os elementos que satisfazem à função booleana. Lembre, o primeiro argumento deve ser uma função booleana (retorna false ou true).
A função anônima pode ter duas variáveis. Por exemplo, para associar elementos de duas listas, podemos usar o comando
zip
:
| > |
![L1, L2 := [1, 2, 3], [4, 5, 6]](images/curso6_117.gif) |
![[1, 2, 3], [4, 5, 6]](images/curso6_118.gif) |
(1.3.3) |
| > |
![zip(proc (x, y) options operator, arrow; [x, y] end proc, L1, L2)](images/curso6_119.gif) |
![[[1, 4], [2, 5], [3, 6]]](images/curso6_120.gif) |
(1.3.4) |
O primeiro operando do comando zip deve ser uma função de duas variáveis. A primeira variável assume valores em L1 (segundo operando) e a segunda variável assume valores em L2 (terceiro operando). O comando zip também pode ser usado com vetores e matrizes, porém não deve ser usado com conjuntos.
Álgebra e Composição de Funções (@ e @@)
Podemos somar, multiplicar e compor duas ou mais funções. Por exemplo, se temos uma equação e queremos subtrair o lado direito do lado esquerdo podemos usar a soma das funções lhs e rhs:
| > |
 |
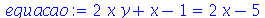 |
(1.4.1) |
| > |
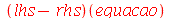 |
 |
(1.4.2) |
O último comando é equivalente a
| > |
 |
 |
(1.4.3) |
porém tem um sentido diferente. No primeiro caso, fizemos uma subtração de funções antes de aplicar ao argumento. No segundo caso fizemos uma subtração usual de expressões algébricas.
Vejamos outros exemplos. Vamos elevar a função seno ao quadrado e depois aplicá-lo ao ponto  .
.
| > |
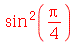 |
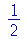 |
(1.4.4) |
Vejamos agora como fazer composição de funções dentro das álgebra de funções.
| > |
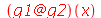 |
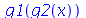 |
(1.4.5) |
| > |
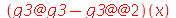 |
 |
(1.4.6) |
O símbolo @ é o operador de composição de funções enquanto que F@@n quer dizer F@F@F... n vezes. Isso explica porque o último resultado é zero. O primeiro resultado, por sua vez, deu o que é esperado, pois composição de funcões é equivalente a aplicação sucessivas das funções. Vejamos outros exemplos:
| > |
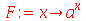 |
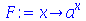 |
(1.4.7) |
| > |
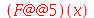 |
 |
(1.4.8) |
| > |
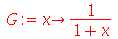 |
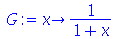 |
(1.4.9) |
| > |
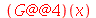 |
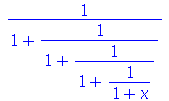 |
(1.4.10) |
| > |
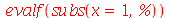 |
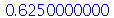 |
(1.4.11) |
| > |
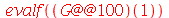 |
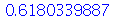 |
(1.4.12) |
Se o operador @@ for usado com um número negativo, o Maple entende que a função inversa deve ser usada:
| > |
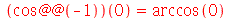 |
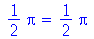 |
(1.4.13) |
Exercício
Defina a função 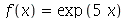 usando o operador seta. Calcule a segunda derivada no ponto 0 usando o operador D. Calcule a segunda derivada usando o comando diff e substitua o valor de
usando o operador seta. Calcule a segunda derivada no ponto 0 usando o operador D. Calcule a segunda derivada usando o comando diff e substitua o valor de 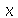 por 0. Os resultados são iguais?
por 0. Os resultados são iguais?
Integral
A integral indefinida de uma expressão pode ser obtida com o comando
int
, por exemplo
| > |
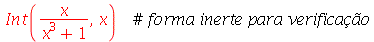 |
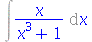 |
(2.1) |
| > |
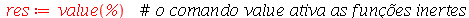 |
 |
(2.2) |
Podemos confirmar o resultado da seguinte forma:
| > |
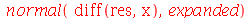 |
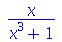 |
(2.3) |
Na integral definida, os limites de integração devem ser especificados da seguinte forma:
| > |
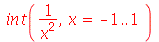 |
 |
(2.4) |
Podemos ver que o Maple reconhece que há uma descontinuidade na função 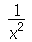 dentro dos limites de integração e calcula corretamente a integral.
dentro dos limites de integração e calcula corretamente a integral.
O método usado para calcular uma integral definida é exato. Para realizar uma integração numérica aproximada, usamos a opção numeric:
| > |
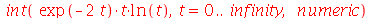 |
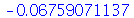 |
(2.5) |
Outra forma é usar a forma inerte do comando int e depois evalf (veja
evalf/int
).
| > |
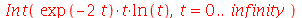 |
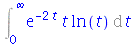 |
(2.6) |
| > |
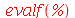 |
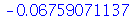 |
(2.7) |
Integrais múltiplas podem ser calculadas com um único comando int usando a seguinte sintaxe:
| > |
![int(f(x, y), [x = a .. b, y = c .. d])](images/curso6_165.gif) |
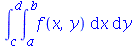 |
(2.8) |
Diversos comando para manipulação com integrais podem ser encontrados no pacote
IntegrationTools
:
| > |
 |
![[Change, CollapseNested, Combine, Expand, ExpandMultiple, Flip, GetIntegrand, GetOptions, GetParts, GetRange, GetVariable, Parts, Split, StripOptions]](images/curso6_168.gif)
![[Change, CollapseNested, Combine, Expand, ExpandMultiple, Flip, GetIntegrand, GetOptions, GetParts, GetRange, GetVariable, Parts, Split, StripOptions]](images/curso6_169.gif) |
(2.9) |
Por exemplo, para divider o intervalo de integração:
| > |
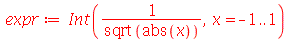 |
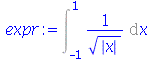 |
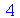 |
(2.10) |
| > |
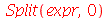 |
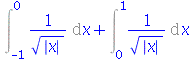 |
(2.11) |
Séries
O comando para expandir em séries é series. Por exemplo
| > |
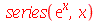 |
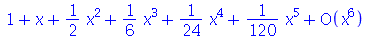 |
(3.1) |
O primeiro operando deve ser a expressão a ser expandida, o segundo é a variável, e o terceiro controla a ordem da expansão:
| > |
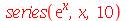 |
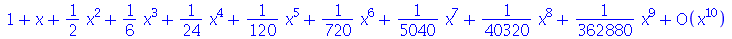 |
(3.2) |
Se o terceiro argumento estiver ausente, o Maple usa o valor da variável global
Order
, que por default é 6. O resultado do comando series é uma estrutura especial que deve ser manipulada pelo próprio comando series. Por exemplo
| > |
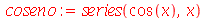 |
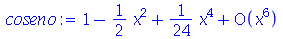 |
(3.3) |
| > |
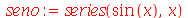 |
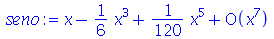 |
(3.4) |
O comando expand nada pode fazer com essas expressões.
| > |
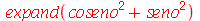 |
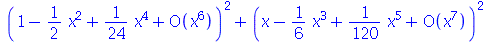 |
(3.5) |
A forma correta é usar o próprio comando series.
| > |
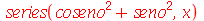 |
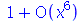 |
(3.6) |
| > |
 |
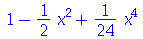 |
(3.7) |
Note que o term 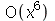 foi eliminado. Agora os termos de ordem 6 ou superior não serão eliminados quando essa expressão for manipulada a menos que voltemos a usar o comando series. A série de Taylor para funções de várias variáveis é obtida com o comando mtaylor.
foi eliminado. Agora os termos de ordem 6 ou superior não serão eliminados quando essa expressão for manipulada a menos que voltemos a usar o comando series. A série de Taylor para funções de várias variáveis é obtida com o comando mtaylor.
| > |
![mtaylor(sin(`+`(`*`(`^`(x, 2)), `*`(`^`(y, 2)))), [x, y], 8)](images/curso6_191.gif) |
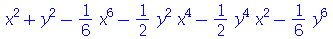 |
(3.8) |
Nesse caso o resultado já é do tipo polinomial.
Séries de Fourier e Transformadas
A série de Fourier de uma função 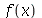 é definida como
é definida como
![f(x) = `+`(`*`(`/`(1, 2), `*`(a[0])), Sum(`+`(`*`(a[n], `*`(cos(`*`(n, `*`(x))))), `*`(b[n], `*`(sin(`*`(n, `*`(x)))))), n = 1 .. infinity))](images/curso6_194.gif)
onde
![a[n] = `/`(`*`(int(`*`(f(x), `*`(cos(`*`(n, `*`(x))))), x = `+`(`-`(Pi)) .. Pi)), `*`(Pi))](images/curso6_195.gif)
![b[n] = `/`(`*`(int(`*`(f(x), `*`(sin(`*`(n, `*`(x))))), x = `+`(`-`(Pi)) .. Pi)), `*`(Pi))](images/curso6_196.gif)
O Maple não tem nenhum comando pré-definido para calcular séries de Fourier. Um programa para esse fim, baseado nas fórmulas acima, é
| > |

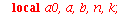
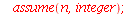



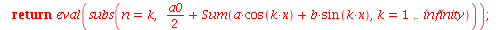
 |
Os comandos proc, local e return são comandos especiais para procedimentos. O comando proc começa um bloco que se fecha no comando end proc. O comando local define variáveis locais ao procedimento de forma a não interferir com as variáveis de mesmo nome utilizadas pelo usuário. Finalmente, o comando return retorna o valor do procedimento. Vejamos um exemplo.
| > |
 |
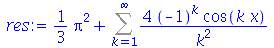 |
(4.1) |
| > |
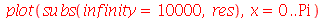 |
As transformadas de funções são calculada após carregar o pacote inttrans (integral transforms).
| > |
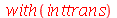 |
![[addtable, fourier, fouriercos, fouriersin, hankel, hilbert, invfourier, invhilbert, invlaplace, invmellin, laplace, mellin, savetable]](images/curso6_210.gif) |
(4.2) |
Por exemplo, a transformada de Laplace de 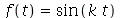 é
é
| > |
 |
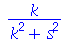 |
(4.3) |
e a transformada inversa é
| > |
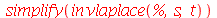 |
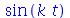 |
(4.4) |
![]() é definida da seguinte maneira.
é definida da seguinte maneira. 
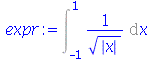
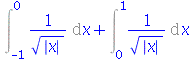
![a[n] = `/`(`*`(int(`*`(f(x), `*`(cos(`*`(n, `*`(x))))), x = `+`(`-`(Pi)) .. Pi)), `*`(Pi))](images/curso6_195.gif)
![b[n] = `/`(`*`(int(`*`(f(x), `*`(sin(`*`(n, `*`(x))))), x = `+`(`-`(Pi)) .. Pi)), `*`(Pi))](images/curso6_196.gif)