| > |
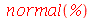 |
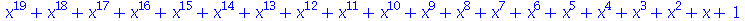 |
(1.4) |
Neste último exemplo temos 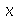 elevado a potência 20, porém poderia ser
elevado a potência 20, porém poderia ser 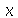 elevado a 1000. A expressão sem fatores comuns ocuparia várias páginas. Qual das formas é a mais simples? Existem situações onde é possivel decidir qual é a forma mais simples. Isto é o que tenta fazer o comando simplify. Em outras situações o próprio usuário deve decidir qual é a forma que ele quer que a expressão seja colocada. Para isso, o Maple possui uma série de comandos de simplificação e manipulação de expressões. São comandos que, quando aplicados a uma expressão, mudam sua forma, mas na maioria das vezes não mudam seu conteúdo. As diferentes formas são matematicamente equivalentes, ou melhor, quase equivalentes. As duas últimas expressões são equivalentes em todos os pontos diferentes de
elevado a 1000. A expressão sem fatores comuns ocuparia várias páginas. Qual das formas é a mais simples? Existem situações onde é possivel decidir qual é a forma mais simples. Isto é o que tenta fazer o comando simplify. Em outras situações o próprio usuário deve decidir qual é a forma que ele quer que a expressão seja colocada. Para isso, o Maple possui uma série de comandos de simplificação e manipulação de expressões. São comandos que, quando aplicados a uma expressão, mudam sua forma, mas na maioria das vezes não mudam seu conteúdo. As diferentes formas são matematicamente equivalentes, ou melhor, quase equivalentes. As duas últimas expressões são equivalentes em todos os pontos diferentes de 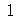 , porém não são equivalentes em
, porém não são equivalentes em 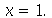
Este capítulo discute um conjunto de comandos que podem axiliar na simplificação de expressões tais como:
simplify - tentar simplificar a expressão matemática.
expand, factor e combine - são comandos mutuamente complementares. expand abre os parênteses executando as propriedades distributivas. factor e combine tentam combinar os termos de modo a agrupar as expressões.
normal - transforma funções racionais para suas formas normais.
Existem diversos outros que executam processamentos mais específicos como dividir polinômios ou expandir uma expressão em frações parciais.
Simplify
Este comando tenta simplificar uma expressão matemática dada aplicando várias regras de transformação. Por ser um comando geral de simplificação, a sua utilização é sempre a primeira tentativa em tornar a expressão mais simples. Pode ser que não faça exatamente a mudança desejada pelo usuário e neste caso outros comandos deverão ser tentados. Os exemplos seguintes mostram algumas aplicações do simplify: Primeiro vamos calcular a terceira derivada da expressão 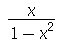 e simplificar o resultado.
e simplificar o resultado.
| > |
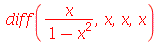 |
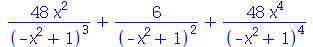 |
(2.1) |
| > |
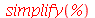 |
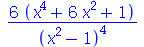 |
(2.2) |
Expressões contendo trigonometria, potência e logarítmos também podem ser simplificadas com suas respectivas propiedades de manipulação.
| > |
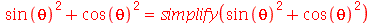 |
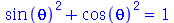 |
(2.3) |
| > |
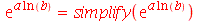 |
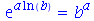 |
(2.4) |
Enquanto estes exemplos fornecem uma boa impressão da funcionalidade do simplify, não é difícil achar exemplos em que a expressão fica menos simples ou que não se altera.
| > |
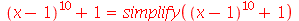 |
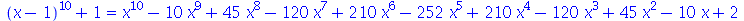 |
(2.5) |
| > |
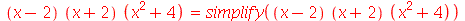 |
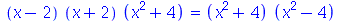 |
(2.6) |
Para expressões na forma 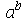 , simplify executa as simplificações que são matematicamente permitidas para quaisquer valores possíveis para a e b. Outras simplificações que, por exemplo, só podem ser realizadas para a > 0, são obtidas com a opção symbolic ou assumindo propriedades com o comando assume.
, simplify executa as simplificações que são matematicamente permitidas para quaisquer valores possíveis para a e b. Outras simplificações que, por exemplo, só podem ser realizadas para a > 0, são obtidas com a opção symbolic ou assumindo propriedades com o comando assume.
| > |
 |
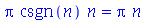 |
(2.7) |
| > |
 |
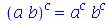 |
(2.8) |
Em muitos contextos, a opção symbolic é muito forte ou não consegue expressar as propriedades matemáticas desejadas. Podemos usar a opção assume
| > |
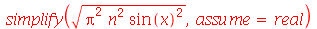 |
 |
(2.9) |
| > |
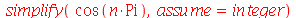 |
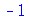 |
(2.10) |
A sintaxe é assume = propriedade, onde propriedade pode ser o nome de um tipo (Maple
type
): real, rational, posint, nonnegint, even, odd, entre centenas de outros nomes ou uma propriedade (veja
property
).
Se o usuário desejar restringir os efeitos do simplify a uma área da expressão, pode-se especificar uma das seguintes opções como parâmetro do comando: exp, GAMMA, hypergeom, ln, polar, power, radical, sqrt e trig. Veja alguns exemplos:
| > |
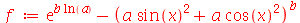 |
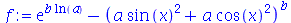 |
(2.11) |
| > |
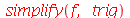 |
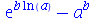 |
(2.12) |
| > |
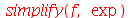 |
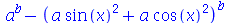 |
(2.13) |
| > |
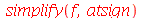 |
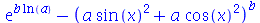 |
(2.14) |
Se uma ou mais equações são fornecidas como parâmetro do simplify, o Maple usa estas informações como vínculos adicionais para simplificar as expressões. Estes vículos podem ser passados como um conjunto, mesmo que tenha apenas um elemento. O background matemático para esta simplificação é representado pelas bases de Gröbner. Pense como seria trabalhoso realizar a simplificação da expressão
| > |
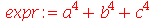 |
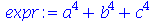 |
(2.15) |
utilizando os seguintes vínculos:
| > |
 |
| > |
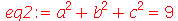 |
| > |
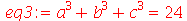 |
O Maple encontra soluções não triviais de primeira (e em pouco tempo):
| > |
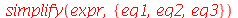 |
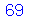 |
(2.17) |
O comando simplify também pode ser usado para eliminar determinadas variáveis de um sistema de equação. No exemplo abaixo,
| > |
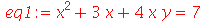 |
| > |
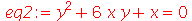 |
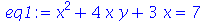 |
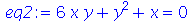 |
(2.18) |
primeiramente vamos eliminar x do sistema de equações
| > |
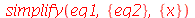 |
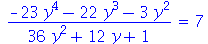 |
(2.19) |
agora vamos eliminar y
| > |
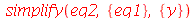 |
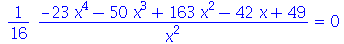 |
(2.20) |
Vamos eliminar a variável a do sistema
| > |
 |
| > |
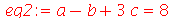 |
| > |
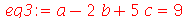 |
| > |
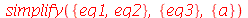 |
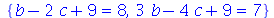 |
(2.22) |
Expand e Normal
O comando expand abre os parênteses contidos na expressão realizando as propriedades distributivas
| > |
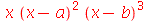 |
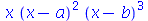 |
(3.1) |
| > |
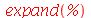 |
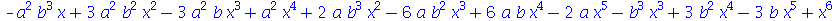 |
(3.2) |
e tem efeito similar quando há potência
| > |
 |
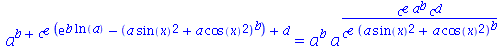 |
(3.3) |
As propriedades trigonométricas também são usadas pelo comando
| > |
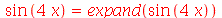 |
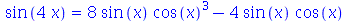 |
(3.4) |
| > |
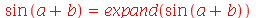 |
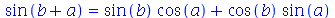 |
(3.5) |
Para funções racionais, só o numerador é alterado
| > |
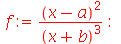 |
| > |
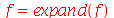 |
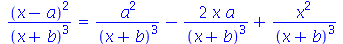 |
(3.6) |
Para que a expansão do denominador também seja feita devemos acessá-lo através do comando denom e processá-lo separado do numerador que é realizado com o comando numer. Esta mesma simplificação pode ser também realizada pelo normal com a opção expanded
| > |
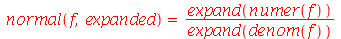 |
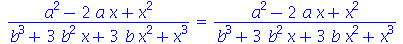 |
(3.7) |
Em certos casos, queremos expandir uma expressão sem expandir um certo pedaço. Para isto, devemos colocar a parte que queremos manter intacta como argumento do comando.
| > |
 |
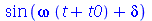 |
(3.8) |
| > |
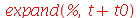 |
 |
(3.9) |
Factor
O comando factor executa o processo inverso do expand tentando converter as várias parcelas de uma soma em um conjunto de produtos
| > |
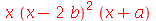 |
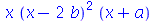 |
(4.1) |
| > |
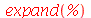 |
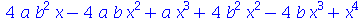 |
(4.2) |
| > |
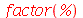 |
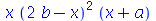 |
(4.3) |
Neste comando a fatorização é feita tanto para o numerador como para o denominador de funções racionais
| > |
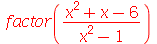 |
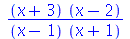 |
(4.4) |
Quando o factor não encontra raízes inteiras, o formato original é mantido. Entretanto, adicionando um argumento pode ajudar o Maple na fatoração
| > |
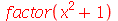 |
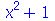 |
(4.5) |
| > |
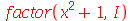 |
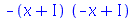 |
(4.6) |
| > |
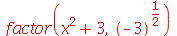 |
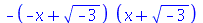 |
(4.7) |
Combine
O combine representa outro comando que executa o processo inverso do expand. Ele tem a finalidade de agrupar funções mais genéricas
| > |
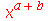 |
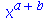 |
(5.1) |
| > |
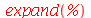 |
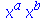 |
(5.2) |
| > |
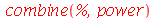 |
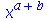 |
(5.3) |
Pode combinar várias raízes em uma só
| > |
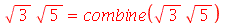 |
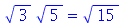 |
(5.4) |
Pode fazer simplificações especificando o tipo ao passar como parâmetreo um dos argumentos: abs, conjugate, exp, ln, plus, power, product, Psi, range, trig e signum
| > |
 |
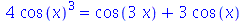 |
(5.5) |
| > |
 |
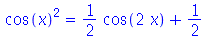 |
(5.6) |
| > |
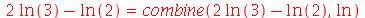 |
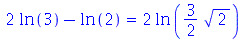 |
(5.7) |
E ainda pode combinar integrais, limites e somas de acordo com seu índices
| > |
 |
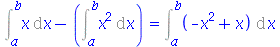 |
(5.8) |
| > |
 |
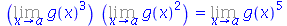 |
(5.9) |
Convert
O comando convert é usado para converter expressões matemáticas em diferentes notações. Estas notações são passadas com argumento para o comando que podem ser: exp, expln, expsincos, ln, sincos, tan, trig, radical, RootOf, factorial, GAMMA entre outros
| > |
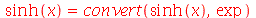 |
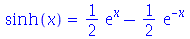 |
(6.1) |
| > |
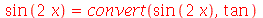 |
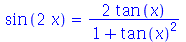 |
(6.2) |
| > |
 |
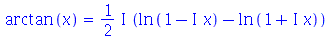 |
(6.3) |
| > |
 |
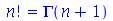 |
(6.4) |
| > |
 |
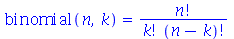 |
(6.5) |
Não existe um comando só para converter uma expressão para frações parciais; ao invés disso o comando convert possui a opção parfrac que realiza esta tarefa. É necessário passar como terceiro argumento a variável na qual se quer modificar
| > |
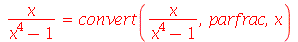 |
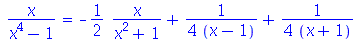 |
(6.6) |
A conversão para frações contínuas também é possível com o auxílio da opção confrac
| > |
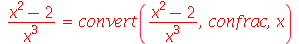 |
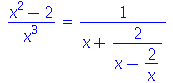 |
(6.7) |
Sort e Collect
O uso destes dois comandos se torna importante quando as expressões são grandes ou quando possuem muitas variáveis. O comando sort reorganiza a expressão ordenando os termos de acordo com a potência
| > |
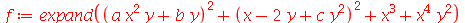 |
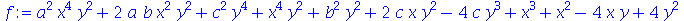 |
(7.1) |
| > |
 |
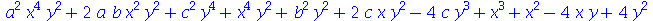 |
(7.2) |
Sem nenhum parâmetro adicional, este comando ordena os termos de acordo com a soma das potências das variáveis de cada parcela. Normalmente a ordenação é feita em relação a uma determinada variável, mas também é possível ordenar para duas
| > |
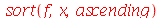 |
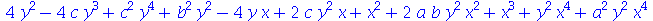 |
(7.3) |
| > |
![sort(f, [x, y])](images/curso3_141.gif) |
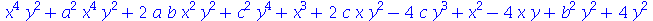 |
(7.4) |
O comando collect possui uma certa afinidade com o comando sort. Ele combina termos que possuem uma variável em comum colocando-a em evidência
| > |
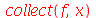 |
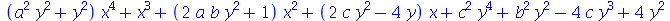 |
(7.5) |
Pode-se escpecificar também duas variáveis para este comando. O critério de associação fica sendo o de colocar em evidência em relação à primeira variável e para os termos resultantes é que será colocada em evidência a segunda variável
| > |
![collect(f, [x, y])](images/curso3_145.gif) |
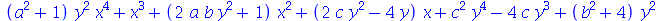 |
(7.6) |
| > |
![collect(f, [y, x])](images/curso3_147.gif) |
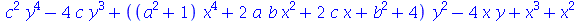 |
(7.7) |
Os dois comandos citados podem trabalhar com funções tais como sin e cos, porém não são capazes de manipular 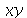 ou
ou 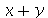
| > |
 |
 |
(7.8) |
| > |
 |
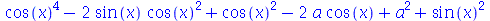 |
(7.9) |
| > |
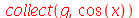 |
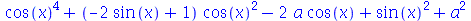 |
(7.10) |
O comando collect pode agrupar derivadas através da opção diff ou D
| > |
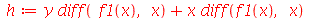 |
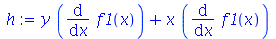 |
(7.11) |
| > |
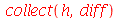 |
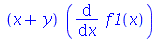 |
(7.12) |
| > |
|
Exercícios
Refs. [1] R. Nicolaides e N. Walkington, Maple a Comprehensive Introduction, [2] Andre Heck, Introduction to Maple
1. Simplifique

2. Expresse
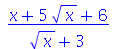
como a soma de um inteiro e um radical.
3. Mostre que
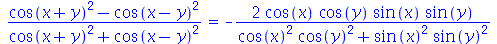
4. Ache a expansão em frações parciais de:
(a) 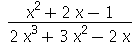
(b) 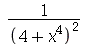
Você consegue simplificar a expressão de modo que ela volte ao formato original?
5. Transforme
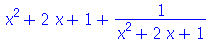
em
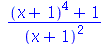
e vice-versa.
6. Considere o polinômio 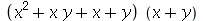 . Use o Maple para transformar em:
. Use o Maple para transformar em:
(a) 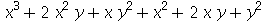
(b) 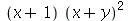
(c) 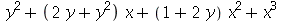
(d) 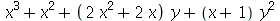
7. Transforme 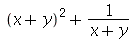 em
em 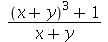 e vice-versa.
e vice-versa.
8. Considere o polinômio 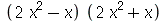 . Use o Maple para transformar em:
. Use o Maple para transformar em:
(a) 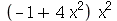
(b) 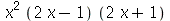
(c) 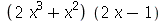
9. Considere a expressão racional 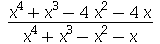 . Transforme a expressão em
. Transforme a expressão em
(a) 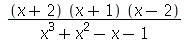
(b) 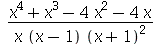
(c) 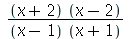
(d) 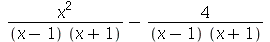
10. Ache o resultado mais simples para a expressão 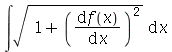 onde
onde 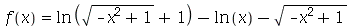 para
para 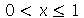 .
.
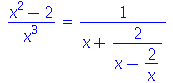
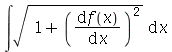 onde
onde